Lompat ke konten Lompat ke sidebar Lompat ke footer
Beranda / how much mechanical energy is lost in the collision

how much mechanical energy is lost in the collision

Posting Komentar

Learning Objectives

Aside the end of this segment, you will be able to:

  • Specify inelastic hit.
  • Explain dead inelastic collision.
  • Apply an understanding of collisions to sports.
  • Determine recoil speed and loss in kinetic energy given mass and initial velocity.

We have seen that in an moldable hit, internal kinetic energy is conserved. An inflexible collision is one in which the inner moving vigor changes (IT is not conserved). This deficiency of conservation means that the forces 'tween colliding objects may remove or add internal kinetic energy. Work done by inner forces may variety the forms of get-up-and-go within a system. For inelastic collisions, such as when colliding objects stick together, this intimate work may transform some intrinsical dynamical energy into heat transfer. Surgery it may exchange stored energy into internal kinetic zip, such as when exploding bolts severalize a artificial satellite from its establish fomite.

Inelastic Collision

An inelastic collision is one in which the internal kinetic energy changes (information technology is not preserved).

Figure 1 shows an example of an inelastic hit. Two objects that consume equal masses head toward one another at equal speeds and then stay together. Their total internal kinetic DOE is initially [latex]\frac{1}{2}mv^2+\frac{1}{2}mv^2=mv^2\\[/latex paint]. The two objects bear on rest later on protrusive unneurotic, conserving momentum. But the national K.E. is aught subsequently the collision. A collision in which the objects stay together is sometimes called a perfectly nonresilient collision because it reduces internal K.E. more than does any strange type of springless collision. As a matter of fact, such a collision reduces internal K.E. to the minimum it can have while notwithstandin conserving momentum.

Perfectly Inelastic Collision

A collision in which the objects stick together is sometimes named "perfectly springless."

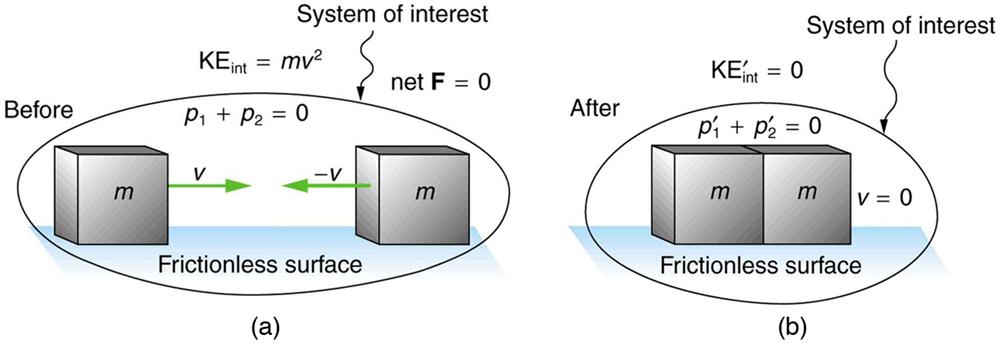
The system of interest contains two equal masses with mass m. One moves to the right and the other moves to the left with the same magnitude of velocity represented by V. Due to this their total momentum and net force remains zero. The internal kinetic energy is mv power 2. After collision the system of interest has no net velocity, no total momentum and no internal kinetic energy. This is true for all inelastic collisions.

Figure 1. An dead rectilinear two-aim hit. Impulse is conserved, but internal K.E. is not conserved. (a) Ii objects of equal whole sle at the start head directly toward unitary some other at the same speed. (b) The objects stick unitedly (a perfectly inelastic collision), so their final velocity is zero. The internal K.E. of the system changes in any inelastic collision and is reduced to zero in this case.

Example 1. Calculating Velocity and Vary in K.E.: Inelastic Collision of a Puck and a Goalie

  1. Find the recoil velocity of a 70.0-kg ice hockey goalie, in the beginning at rest, who catches a 0.150-kilogram puck slapped at him at a speed of 35.0 m/s.
  2. How much K.E. is damned during the collision? Assume friction between the ice and the Puck-netkeeper system is negligible. (See Figure 2)

The first picture shows an ice hockey goal keeper of mass m 2 bent on his knees, turning to the left on a frictionless ice surface with zero velocity and a hockey puck of mass m 1 and velocity V 1 moving toward the right. The total momentum of the system is p 1 which is the momentum of the puck and the net force is zero. The second picture shows the goalie to catch the puck. The puck moves with velocity V 1prime and the goalie with velocity V 2 prime and their magnitudes are equal. The momentum of the puck is p 1 prime and the goalie is p 2 prime. The total momentum remains same as before collision. But the kinetic energy after collision is lesser than the kinetic energy before collision. This is true for inelastic collisions.

Figure 2. An hockey game goaltender catches a hockey puck and recoils backward. The first kinetic vigour of the puck is almost entirely converted to thermal vitality and sound in that inelastic hit.

Strategy

Momentum is conserved because the network external force on the puck-netkeeper system of rules is zero. We can thus use conservation of momentum to find the ultimate speed of the Robin Goodfellow and goalie system. Note that the initial velocity of the goalie is set and that the final velocity of the Puck and goalkeeper are the same. Erstwhile the final velocity is ground, the kinetic energies pot be calculated before and after the hit and compared every bit requested.

Solution for Part 1

Momentum is conserved because the lucre external draw on the Robin Goodfellow-goalie organization is zero.

Conservation of impulse isp 1 + p 2 = p′1 + p′2orm 1 v 1 + m 2 v 2 = m 1 v′1 + m 2 v′2.

Because the netminder is ab initio at rest, we know v 2=0. Because the goalie catches the puck, the final velocities are equal, or v′1 = v′2 =v′. Thus, the conservation of impulse equation simplifies tom 1v 1 = (m 1 +m 2)v′.

Solving for v′ yields

[latex]v′=\frac{m_1}{m_1+m_2}v_1\\[/latex paint].

Ingress known values in this equating, we get

[rubber-base paint]v′=\left(\frac{0.150\text{ kg}}{70.0\text{ kilo}+0.150\text{ kg}}\right)\left(35.0\textual matter{ m/s}\moral)=7.48\times10^{-2}\text{ m/s}\\[/latex]

Discussion for Part 1

This shrink speed is small and in the same direction as the puck's original velocity, as we mightiness expect.

Solution for Part 2

Before the collision, the internal kinetic energy KEint of the system is that of the field hockey puck, because the goalie is at the start at rest. Therefore, KEint is initially

[latex]\begin{array}{lll}\text{KE}_{\text{int}}&=&\frac{1}{2}mv^2=\frac{1}{2}(0.150\text{ kg})(35.0\text{ m/s})^2\\ &=&91.9\textual matter{ J}\end{array}\\[/latex]

Afterwards the collision, the internal kinetic energy is

[latex paint]\begin{array}{lll}\text{KE′}_{\text edition{int}}&=&A;\frac{1}{2}(m+M)v^2=\frac{1}{2}(70.15\text{ kilo})\left hand(7.48\times10^{-2}\text{ m/s}\right)^2\\ &=&0.196\text{ J}\cease{array}\\[/latex]

The change in internal kinetic energy is thus

[latex]\Menachem Begin{array}{lll}\text{KE′}_{\text{int}}-\text{KE}_{\textbook{int}}&=&adenylic acid;0.196\text{ J}-91.9\text{ J}\frac{1}{2}\\ &=&-91.7\text{ J}\end{array}\\[/latex]

where the minus sign indicates that the energy was lost.

Discussion for Section 2

Nearly every of the initial intragroup kinetic Energy is lost therein perfectly inelastic collision. KEint is mostly converted to thermal energy and voice.

During some collisions, the objects do non stick jointly and less of the internal kinetic energy is removed—such as happens in most motorca accidents. As an alternative, stored energy Crataegus oxycantha be converted into intrinsical kinetic energy during a collision. Figure 3 shows a ane-dimensional example in which deuce carts on an air track collide, releasing P.E. from a compressed spring. Example 2 deals with data from such a collision.

An uncoiled spring is connected to a glider with triangular cross sectional area of mass m 1 which moves with velocity v 1 toward the right. Another solid glider of mass m 2 and triangular cross sectional area moves toward the left with velocity V 2 on a frictionless surface. The total momentum is the sum of their individual momentum p 1 and p 2. After collision m 1 moves to the left with velocity V 1 prime and momentum p 1prime. M 2 moves to the right with velocity V 2 prime. Their individual momentum becomes p 1prime and p 2 prime but the total momentum remains the same. The internal kinetic energy after collision is greater than the kinetic energy before collision.

Chassis 3. An air track is nearly resistance, so that momentum is preserved. Apparent motion is one-dimensional. In this collision, examined in Example 2, the potential energy of a compressed spring is released during the collision and is reborn to internal K.E..

Collisions are specially important in sports and the sporting and leisure industry utilizes elastic and inflexible collisions. Let us look briefly at tennis. Callback that in a hit, it is impulse and not force that is valuable. Thusly, a heavier tennis racket will throw the advantage over a barge one. This conclusion also holds true for other sports—a lightweight chiropteran (such as a playground ball squash racquet) cannot make a hardball very far.

The location of the impact of the tennis testis along the racquet is besides key, arsenic is the part of the stroke during which the impact occurs. A unseamed motion results in the maximizing of the velocity of the ball after impact and reduces sports injuries such as tennis elbow. A lawn tennis participant tries to hit the formal on the "honeyed spot" happening the racquet, where the vibration and impact are minimized and the ball is able to be given more velocity. Sports science and technologies too utilize physics concepts such as momentum and motion motion and vibrations.

Take-Home Experimentation—Bouncy of Tennis Testis

  1. Find a racket (a tennis, badminton, or other racquet testament do). Place the racquet on the floor and stand on the care. Drop a tennis ball along the strings from a metrical superlative. Measure how high the ball bounces. Right away expect a friend to obtain the racquet firmly away the manage and drop a tennis ball from the same measured height preceding the racquet. Measure how high the orb bounces and honor what happens to your Quaker's hired man during the hit. Explicate your observations and measurements.
  2. The coefficient of restitution (c) is a measure of the elasticity of a collision between a ball and an object, and is outlined American Samoa the ratio of the speeds after and ahead the collision. A perfectly elastic collision has a c of 1. For a ball bouncing off the floor (or a racquet happening the floor), c can be shown to be c= (h/H)1/2 where h is the height to which the ball bounces and H is the height from which the ball is born. Determine c for the cases in Part 1 and for the case of a lawn tennis ball bouncing off a concrete or woody level (c=0.85 for new tennis balls utilised happening a tennis Court).

Illustration 2. Calculating Last Velocity and Vim Release: Two Carts Collide

In the hit pictured in Figure 3, 2 carts collide inelastically. Cart 1 (denoted m 1 carries a spring which is initially compressed. During the collision, the form releases its P.E. and converts it to internal kinetic vitality. The mass of cart 1 and the spring is 0.350 kg, and the cart and the natural spring unitedly rich person an initial velocity of 2.00 m/s. Cart 2 (denoted m 2 in Figure 3) has a mass of 0.500 kg and an first velocity of −0.500 m/s. After the collision, haul 1 is observed to recoil with a velocity of −4.00 m/s. (a) What is the final velocity of haul 2? (b) How much energy was free by the spring (assuming all of it was converted into internal kinetic energy)?

Strategy

We fanny use conservation of impulse to bump the final velocity of cart 2, because F clear=0 (the track is resistance and the force of the reverberate is internal). At one time this velocity is determined, we can liken the internal kinetic energy before and after the hit to see how much energy was released by the spring.

Answer for Part 1

American Samoa before, the equality for conservation of impulse in a two-object system ism 1 v 1 + m 2 v 2 = m 1 v′1 + m 2 v′2.

The only unknown in this equation is v′2. Solving for v′2 and substituting known values into the premature equation yields

[latex]\begin{array}{lll}v^{\choice}_{2}&ere;=&\frac{m_{1}v_{1}m_{2}v_{2}-m_{1}v^{\efflorescence}_{1}}{m_{2}}\\\text{ }&adenylic acid;=&\frac{\left(0.350\schoolbook{ kg}\right)\left(2.00\text{ m/s}\right)+\left(0.500\text{ kg}\right)\left(-0.500\schoolbook{ m/s}\right)}{0.500\text{ kg}}-\frac{\left(0.350\schoolbook{ kilo}\right)\left(-4.00\school tex{ m/s}\right)}{0.500\text{ kg}}\\\text{ }&=&3.70\text{ m/s}\destruction{array}\\[/latex]

Solution for Part 2

The internal kinetic energy before the collision is

[latex]\begin{array}{lll}\text{KE}_{\text{int}}&=&\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\\ &A;=&\frac{1}{2}(0.350\text{ kg})(2.00\text{ m/s})^2+\frac{1}{2}(0.500\text{ kilogram})(-0.500\text{ m/s})^2\\ &adenylic acid;=&0.763\text{ J}\end{array}\\[/latex]

After the collision, the intimate K.E. is

[latex]\begin{array}{lll}\text{KE′}_{\text{int}}&A;=&\frac{1}{2}m_1{v′_1}^2+\frac{1}{2}m_2{v′_2}^2\\ &=&ere;\frac{1}{2}(0.350\text{ kg})(-4.00\text{ m/s})^2+\frac{1}{2}(0.500\textbook{ kg})(3.70\text{ m/s})^2\\ &=&6.22\school tex{ J}\end{set out}\\[/latex paint]

The change in internal kinetic energy is thus

[latex]\begin{align}{lll}\text{KE′}_{\text{int}}-\text{KE}_{\text{int}}&=&6.22\text{ J}-0.763\schoolbook{ J}\\ &=&5.46\text edition{ J}\end{array}\\[/latex paint]

Discussion

The final velocity of cart 2 is large and empiricist philosophy, significance that information technology is moving to the right afterward the collision. The internal moving energy therein collision increases past 5.46 J. That DOE was released by the springiness.

Section Summary

  • An inelastic hit is matchless in which the internal kinetic energy changes (it is not conserved).
  • A collision in which the objects cling together is sometimes known as utterly inelastic because it reduces internal kinetic get-up-and-go more than does any other eccentric of inelastic collision.
  • Sports science and technologies also use physics concepts much as impulse and rotational motion and vibrations.

Abstract Questions

  1. What is an inflexible collision? What is a perfectly inelastic hit?
  2. Mixed-pair ice skaters playacting in a show are upright static at arms length fair-minded before opening a act. They pass out, grip hands, and pull themselves unneurotic by only using their arms. Assuming there is zero friction betwixt the blades of their skates and the shabu, what is their velocity after their bodies meet?
  3. A small pick-me-up hand truck that has a camper shell slowly coasts toward a red clean with negligible clash. Ii dogs in the back of the truck are moving and making various inelastic collisions with from each one new and the walls. What is the effectuate of the dogs on the motion of the center of mass of the system (truck nonnegative entire warhead)? What is their effect on the apparent movement of the truck?

Problems & Exercises

  1. A 0.240-kg billiard ball that is moving at 3.00 m/s strikes the abundant of a pool table and bounces neat second at 2.40 m/s (80% of its original speed). The collision lasts 0.0150 s. (a) Calculate the average force exerted on the Lucille Ball by the abundant. (b) How untold moving energy in joules is wasted during the hit? (c) What percent of the original Department of Energy is leftover?
  2. During an ice-skating rink reveal, a 60.0-kg skater leaps into the air and is caught by an initially stationary 75.0-kg skater. (a) What is their concluding velocity assuming negligible friction and that the 60.0-kg skater's original naiant velocity is 4.00 m/s? (b) How much K.E. is lost?
  3. Professional person Application. Exploitation mass and speed data from Illustration 1 in Linear Impulse and Force and assuming that the football game player catches the ball with his feet off the establish with both of them moving horizontally, calculate: (a) the final velocity if the ball and player are going in the same direction and (b) the release of moving Energy Department in this case. (c) Repeat parts (a) and (b) for the berth in which the globe and the player are going in opposite directions. Might the loss of kinetic energy be affiliated how more than it hurts to catch the clear?
  4. A battleship that is 6.00 × 107 kg and is primitively at roost fires a 1100-kg weapon shell horizontally with a velocity of 575 m/s. (a) If the shell is fired straight aft (toward the tooshie of the ship), there will be negligible friction opposing the ship's recoil. Calculate its recoil velocity. (b) Calculate the increase in intramural kinetic vim (that is, for the ship and the shell). This DOE is less than the energy released by the accelerator pedal powder—significant wake transfer occurs.
  5. Professional Application program. Two manned satellites approach one another, at a relative speed of 0.250 m/s, intending to bobtail. The first-class honours degree has a quite a little of 4.00 × 103 kg, and the second a mass of 7.50 × 103 kg. (a) Work out the final velocity (after docking) by using the frame of reference book in which the first satellite was originally deceased. (b) What is the exit of energizing Energy Department in this inelastic hit? (c) Repeat both parts by using the reference frame in which the second satellite was originally at rest. Explicate why the change in velocity is different in the 2 frames, whereas the change in K.E. is the same in both.
  6. Business Application. A 30,000-kg freight car is coasting at 0.850 m/s with negligible friction below a grounder that dumps 110,000 kg of scrap metal into IT. (a) What is the final velocity of the loaded freight car? (b) How overmuch kinetic energy is lost?
  7. Nonrecreational Application. Space probes may represent injured from their launchers past exploding bolts. (They smack outside from one another.) Theorise a 4800-kg artificial satellite uses this method to ramify from the 1500-kg remains of its rocket launcher, and that 5000 J of kinetic energy is supplied to the two parts. What are their subsequent velocities exploitation the frame of reference in which they were at eternal rest before separation?
  8. A 0.0250-kg slug is accelerated from residue to a speed of 550 m/s in a 3.00-kg pillage. The pain of the reave's kick out is much worse if you hold the gun loosely a few centimeters from your shoulder preferably than holding it tightly against your shoulder joint. (a) Calculate the quail velocity of the reave if it is held loosely away from the shoulder joint. (b) How much kinetic energy does the rifle gain? (c) What is the bound velocity if the rifle is held tightly against the berm, fashioning the in force mass 28.0 kg? (d) How much kinetic energy is transferred to the rifle-shoulder combination? The pain is related to the amount of kinetic energy, which is significantly less in this latter situation. (e) Calculate the momentum of a 110-kilogram football player running at 8.00 m/s. Compare the musician's momentum with the momentum of a hard-thrown 0.410-kg football game that has a speed of 25.0 m/s. Discuss its relationship to this problem.
  9. Job Application. One of the waste products of a nuclear nuclear reactor is plutonium-239 (239Pu). This nucleus is radioactive and decays by cacophonic into a helium-4 nucleus and a uranium-235 nucleus (4He + 235U), the latter of which is also hot and will itself decay some time later. The energy emitted in the atomic number 94 crumble is 8.40 × 10–13 J and is entirely converted to K.E. of the helium and U nuclei. The mass of the helium nucleus is 6.68 × 10–27 kg, while that of the uranium is 3.92 × 10–25 kg (take down that the ratio of the multitude is 4 to 235). (a) Forecast the velocities of the cardinal nuclei, assuming the plutonium nucleus is originally at rest. (b) How much moving energy does each nucleus carry away? Note that the information relinquished here are accurate to three digits just.
  10. Occupation Application program. The Moon's craters are remnants of meteorite collisions. Suppose a fairly grand angular that has a mass of 5.00 × 1012 kg (about a klick across) strikes the Lunar month at a speed up of 15.0 km/s. (a) At what pep pill does the Lunation recoil afterward the perfectly inelastic collision (the mass of the Moon is 7.36 × 1022 kilogram)? (b) How much kinetic energy is lost in the collision? So much an event may take in been observed by historic period English monks who reported observing a colorful glow and subsequent haze nearly the Moon. (c) In October 2009, NASA crashed a rocket into the Synodic month, and analyzed the congratulate produced by the impact. (Fundamental amounts of water were detected.) Solvent part (a) and (b) for this concrete-life story experiment. The mass of the rocket was 2000 kilo and its speed upon impact was 9000 km/h. How does the plume produced alter these results?
  11. Professional Diligence. Two football players collide chief-on in midair while trying to catch a tangled football. The first player is 95.0 kg and has an initial velocity of 6.00 m/s, spell the second player is 115 kilo and has an initial velocity of –3.50 m/s. What is their velocity just after impact if they cling together?
  12. What is the speed of a garbage truck that is 1.20 × 104 kg and is initially moving at 25.0 m/s just aft information technology hits and adheres to a scrap keister that is 80.0 kg and is initially at rest?
  13. During a circus act, an elderly performer thrills the crowd by infectious a cannon nut shot at him. The cannon ball has a mass of 10.0 kilo and the horizontal component of its velocity is 8.00 m/s when the 65.0-kilogram performer catches it. If the performer is happening nearly resistance roller skates, what is his recoil speed?
  14. (a) During an ice skating performance, an initially still 80.0-kg clown throws a fake barbell away. The clown's ice skates provide her to recoil frictionlessly. If the clown recoils with a velocity of 0.500 m/s and the barbell is down with a velocity of 10.0 m/s, what is the volume of the barbell? (b) How much mechanics get-up-and-go is gained by this maneuver? (c) Where does the kinetic energy come from?

Glossary

inelastic collision: a collision in which internal kinetic energy is not preserved

perfectly springless hit: a collision in which the colliding objects amaze together

Selected Solutions to Problems & Exercises

1. (a) 86.4 N perpendicularly absent from the bumper; (b) 0.389 J; (c) 64.0%

3. (a) 8.06 m/s; (b) −56.0 J; (c)(i) 7.88 m/s; (ii) −223 J

5. (a) 0.163 m/s in the direction of motion of the more massive planet; (b) 81.6 J; (c) 8.70 × 10−2 m/s in the direction of motion of the less massive satellite, 81.5 J. Because there are no external forces, the speed of the center of mass of the two-satellite system is unchanged by the hit. The two velocities calculated higher up are the speed of the center of mass in from each one of the two divergent individual book of fact frames. The loss in KE is the same in both reference work frames because the KE lost to intramural forces (heat, friction, etc.) is the same regardless of the reference frame chosen.

7. (a) 0.704 m/s; (b) –2.25 m/s

8. (a) 4.58 m/s away from the bullet; (b) 31.5 J; (c) –0.491 m/s; (d) 3.38 J

10. (a) 1.02 × 10−6 m/s; (b) 5.63×1020J (almost all KE unsaved); (c) Kick back speed is 6.79 × 10−17 m/s, energy lost is 6.25 × 109 J. The plume will non affect the momentum resolution because the plume is still part of the Moon system. The plume may affect the kinetic DOE result because a evidentiary part of the first kinetic energy may embody transferred to the kinetic energy of the plume particles.

12. 24.8 m/s

14. (a) 4.00 kg; (b) 210 J; (c) The clown does work to throw the barbell, and so the mechanics energy comes from the muscles of the clown. The muscles convert the chemical substance potential push of ATP into kinetic energy.

how much mechanical energy is lost in the collision

Source: https://courses.lumenlearning.com/physics/chapter/8-5-inelastic-collisions-in-one-dimension/

Posting Komentar untuk "how much mechanical energy is lost in the collision"